「勝利の方程式」を数学で解くことは可能!? いやでも数学が面白くなる“大人の学び直し”
公開日:2019/5/14

気づけば、数学がきらいになっていた。きっかけは中学1年生のときだろう。一次方程式で授業についていけなくなり、宿題をやろうにもできない。当然、先生には怒られる。挽回する糸口が見いだせないまま、テストを迎え、見事に撃沈…。「数学なんかできなくたって人生やっていける!」、そう思い込んでしまった私のように、数学に対して苦手意識を持ったまま大人になった人は少なくないだろう。
そんなときには、堅苦しい勉強という形ではなく「数学って面白いかも」と思える体験からやり直しをしなくてはいけないだろう。そう考える人にぴったりの1冊が、『いやでも数学が面白くなる 「勝利の方程式」は解けるのか?(ブルーバックス)』(志村史夫/講談社)だ。
本書は、数学が苦手だったという人にも学び直しのきっかけを与えてくれる。学生の頃のようにただ公式を覚えて問題を解く、という勉強ではなく、学校で教わった数学が「こんなに役に立つのか!」という事例や豆知識などを説明してくれるのだ。もちろん、数学が得意だという人も改めて「数学って色々なところで生活と結びついているんだなぁ…」という発見ができるはずだ。
■「0(ゼロ)」はとても偉大な発見だった!
現在は日常生活で当たり前のように使っている「0(ゼロ)」。しかし、数学史上ではかなり画期的な発見だったという。ゼロが存在することによって、私たちが小学校で習った筆算が可能となり、ゼロが基準となるからこそ「+(プラス)と-(マイナス)の概念」が生まれ、2進法を使ったコンピューターも開発された。
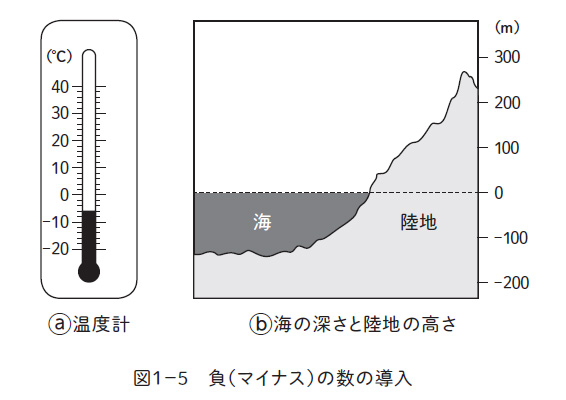
もし、ゼロが存在せず、マイナスという概念がなかったら、図のような気温や深さ・高さの表記もできない。もしなかったら…。とにかく、ゼロが偉大であることは理解できた。今度、「0(ゼロ)」と書くときはもっと丁寧に書いてあげたい。
■算数と数学の違いはどこにある?
小学校で習うのが算数で、中学以降で習うのが数学であることは間違いない。だが、「やっている内容はあんまり変わらないのだから、統一すればいいのに…」と考えてしまうのが常だろう。
だが実は、この2つには明確な違いがあるのだという。それは数字以外の文字を使うかどうか、なのだとか。つまり、XやYといった文字を使って方程式を作れるのが数学ということだ。
具体的な数字の代わりに文字を使って「物事を一般化して考える」こと。これが、数学を勉強する意義であり、真髄であるという。数学、奥深し…。
■世界一有名なアインシュタインの方程式
数学アレルギーに近い私でも知っているのが、アインシュタインの数式だ。
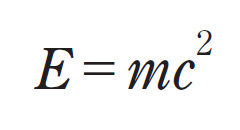
知ってはいるものの、それが何を指しているのかチンプンカンプンだ。アインシュタインは、特殊相対性理論の帰結としてこの数式を導いた。これを言葉で表すとこのようになる。

すぐピンとこないかもしれないが、石油や石炭を燃やすことでエネルギーが生まれるように、「物質からエネルギーが生まれる」ということを指している。この数式は、原子力発電や、人体の断面を撮影する医療技術などさまざまな分野で現在応用されている。
そのような数式を少しでも知っていると、ひとつ賢くなった気が確実にするし、もう少し理解できないかな? と前向きに考えられるようになるから不思議だ。
■方程式の「方程」って何だ?
本稿でたびたび出てきた「方程式」。さて、方程式の「方程」という言葉の意味を知っているだろうか? 方程とは、「数量を並べて比べる」ことだそうだ。
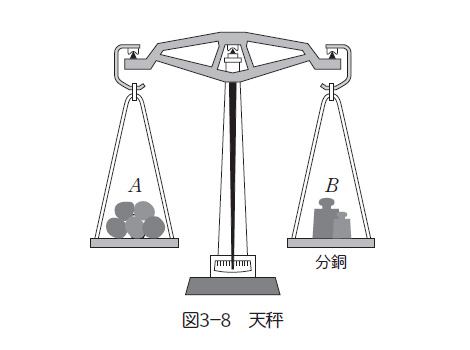
図のような天秤をイメージしてみよう。天秤の片方に重さのわからないモノ(A)を乗せ、もう片方に分銅(B)を乗せて重さを釣り合わせることで、わからなかった重さがわかる。
方程式の原則は天秤が釣り合っている形にそっくりだ。方程式は=(イコール)という記号で左右が結ばれているが、これは左辺と右辺は同じ数であることを表している。つまり「X=5」という式ならば「5=5」と同じ意味になる。
この考え方が分かれば、方程式で欠かせない「移項」によって+や-が変化することも説明がつく。理屈がわからずに問題を解いていた人も多いはずだ。
ちなみに、野球やスポーツ解説で「勝利の方程式」という言葉がよく使われる。これが実は理屈に合っていない“造語”なのだと、方程式の意味を理解していればわかるはずだ。
数学が苦手、という人にとって、本書の全ての内容をすぐに理解することは難しいかもしれない。私も一度目に読んだ際は、どうしてもわからない箇所はサラッと読み、先に進んでしまった。だが、これでも良いのではと思う。本書の目的は数学ぎらいを和らげること、そして「数学って面白いかも。もう少し勉強してみようかな…」と感じることにあるはずだ。
肩肘張り過ぎで読むのでなく、「これ面白いじゃん!」と思える発見を本書を通じてしてみよう。それこそが、学生にはできない、大人の勉強の特権だ。
文=冴島友貴





